►Math Library
▼7 Matrices and Linear Algebra
On this page:
matrix
row-matrix
col-matrix
identity-matrix
make-matrix
build-matrix
diagonal-matrix
block-diagonal-matrix
vandermonde-matrix
for/  matrix:
for*/  matrix:
for/  matrix
for*/  matrix
  top  ← prev  up  next → 

7.3 Construction

syntax

(matrix [[expr ...+] ...+] maybe-type-ann)

 
maybe-type-ann = 
  | : type
Like the array form for creating arrays, but does not require #[...] to delimit nested rows, and the result is constrained to be a matrix?.

Examples:
> (matrix [[1 2 3] [4 5 6]])

- : (Array Positive-Byte)

(array #[#[1 2 3] #[4 5 6]])

> (matrix [[1 2 3] [4 5 6]] : Number)

- : (Array Number)

(array #[#[1 2 3] #[4 5 6]])

> (matrix [[]])

eval:20:0: matrix: given empty row

  at: ()

  in: (matrix (()))

syntax

(row-matrix [expr ...+] maybe-type-ann)

 
maybe-type-ann = 
  | : type
Like matrix, but returns a row matrix.

Examples:
> (row-matrix [1 2 3])

- : (Array Positive-Byte)

(array #[#[1 2 3]])

> (row-matrix [1 2 3] : Number)

- : (Array Number)

(array #[#[1 2 3]])

> (row-matrix [])

eval:23:0: row-matrix: given empty row

  at: ()

  in: (row-matrix ())

syntax

(col-matrix [expr ...+] maybe-type-ann)

 
maybe-type-ann = 
  | : type
Like matrix, but returns a column matrix.

Examples:
> (col-matrix [1 2 3])

- : (Array Positive-Byte)

(array #[#[1] #[2] #[3]])

> (col-matrix [1 2 3] : Number)

- : (Array Number)

(array #[#[1] #[2] #[3]])

> (col-matrix [])

eval:26:0: col-matrix: given empty column

  at: ()

  in: (col-matrix ())

procedure

(identity-matrix n [one zero]) → (Matrix A)

  n : Integer
  one : A = 1
  zero : A = 0
Returns an n×n identity matrix, which has the value one on the diagonal and zero everywhere else. The height/width n must be positive.

Examples:
> (identity-matrix 3)

- : (Array (U One Zero))

(array #[#[1 0 0] #[0 1 0] #[0 0 1]])

> (identity-matrix 4 1.0+0.0i 0.0+0.0i)

- : (Array Float-Complex)

(array

 #[#[1.0+0.0i 0.0+0.0i 0.0+0.0i 0.0+0.0i]

   #[0.0+0.0i 1.0+0.0i 0.0+0.0i 0.0+0.0i]

   #[0.0+0.0i 0.0+0.0i 1.0+0.0i 0.0+0.0i]

   #[0.0+0.0i 0.0+0.0i 0.0+0.0i 1.0+0.0i]])

procedure

(make-matrix m n x) → (Matrix A)

  m : Integer
  n : Integer
  x : A
Returns an m×n matrix filled with the value x; both m and n must be positive. Analogous to make-array (and defined in terms of it).

procedure

(build-matrix m n proc) → (Matrix A)

  m : Integer
  n : Integer
  proc : (Index Index -> A)
Returns an m×n matrix with entries returned by proc; both m and n must be positive. Analogous to build-array (and defined in terms of it).

procedure

(diagonal-matrix xs [zero]) → (Matrix A)

  xs : (Listof A)
  zero : A = 0
Returns a matrix with xs along the diagonal and zero everywhere else. The length of xs must be positive.

Examples:
> (diagonal-matrix '(1 2 3 4 5 6))

- : (Array Byte)

(array

 #[#[1 0 0 0 0 0]

   #[0 2 0 0 0 0]

   #[0 0 3 0 0 0]

   #[0 0 0 4 0 0]

   #[0 0 0 0 5 0]

   #[0 0 0 0 0 6]])

> (diagonal-matrix '(1.0 2.0 3.0 4.0 5.0) 0.0)

- : (Array (U Flonum-Positive-Zero Positive-Float-No-NaN))

(array

 #[#[1.0 0.0 0.0 0.0 0.0]

   #[0.0 2.0 0.0 0.0 0.0]

   #[0.0 0.0 3.0 0.0 0.0]

   #[0.0 0.0 0.0 4.0 0.0]

   #[0.0 0.0 0.0 0.0 5.0]])

procedure

(block-diagonal-matrix Xs [zero]) → (Matrix A)

  Xs : (Listof (Matrix A))
  zero : A = 0
Wikipedia: Block-diagonal matrices Returns a matrix with matrices Xs along the diagonal and zero everywhere else. The length of Xs must be positive.

Examples:
> (block-diagonal-matrix (list (matrix [[6 7] [8 9]])
                               (diagonal-matrix '(7 5 7))
                               (col-matrix [1 2 3])
                               (row-matrix [4 5 6])))

- : (Array Byte)

(array

 #[#[6 7 0 0 0 0 0 0 0]

   #[8 9 0 0 0 0 0 0 0]

   #[0 0 7 0 0 0 0 0 0]

   #[0 0 0 5 0 0 0 0 0]

   #[0 0 0 0 7 0 0 0 0]

   #[0 0 0 0 0 1 0 0 0]

   #[0 0 0 0 0 2 0 0 0]

   #[0 0 0 0 0 3 0 0 0]

   #[0 0 0 0 0 0 4 5 6]])

> (block-diagonal-matrix (list (make-matrix 2 2 2.0+3.0i)
                               (make-matrix 2 2 5.0+7.0i))
                         0.0+0.0i)

- : (Array Float-Complex)

(array

 #[#[2.0+3.0i 2.0+3.0i 0.0+0.0i 0.0+0.0i]

   #[2.0+3.0i 2.0+3.0i 0.0+0.0i 0.0+0.0i]

   #[0.0+0.0i 0.0+0.0i 5.0+7.0i 5.0+7.0i]

   #[0.0+0.0i 0.0+0.0i 5.0+7.0i 5.0+7.0i]])

procedure

(vandermonde-matrix xs n) → (Matrix Number)

  xs : (Listof Number)
  n : Integer
Wikipedia: Vandermonde matrix Returns an m×n Vandermonde matrix, where m = (length xs).

Examples:
> (vandermonde-matrix '(1 2 3 4) 5)

- : (Array Real)

(array #[#[1 1 1 1 1] #[1 2 4 8 16] #[1 3 9 27 81] #[1 4 16 64 256]])

> (vandermonde-matrix '(5.2 3.4 2.0) 3)

- : (Array Flonum)

(array

 #[#[1.0 5.2 27.040000000000003]

   #[1.0 3.4 11.559999999999999]

   #[1.0 2.0 4.0]])

Using a Vandermonde matrix to find a Lagrange polynomial (the polynomial of least degree that passes through a given set of points):
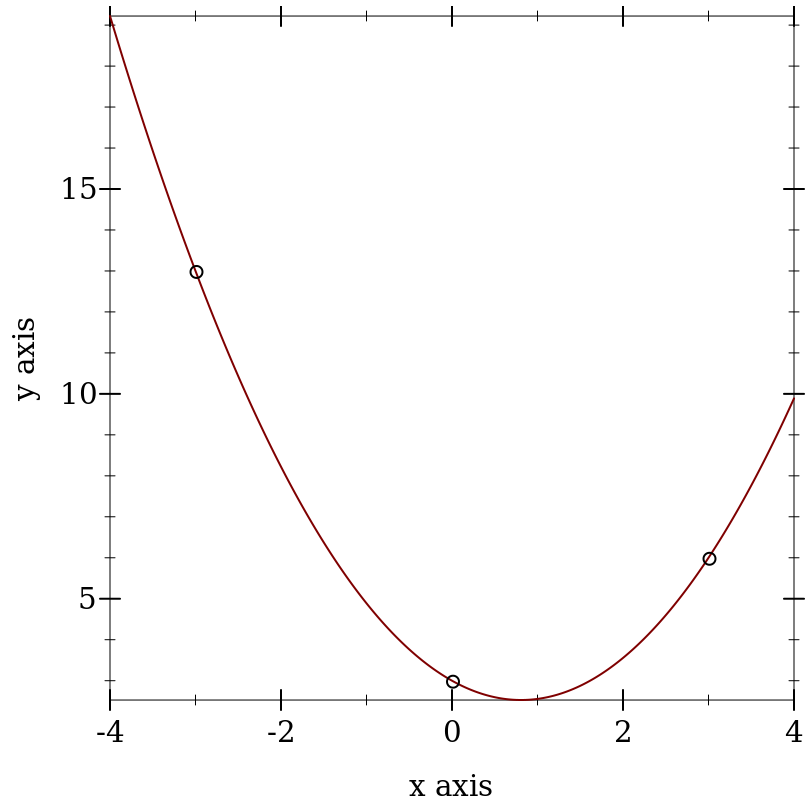
> (define (lagrange-polynomial xs ys)
    (array->list (matrix-solve (vandermonde-matrix xs (length xs))
                               (->col-matrix ys))))
> (define xs '(-3 0 3))
> (define ys '(13 3 6))
> (match-define (list c b a) (lagrange-polynomial xs ys))
> (plot (list (function (λ (x) (+ c (* b x) (* a x x))) -4 4)
              (points (map list xs ys))))

image

Note that the above example is in untyped Racket.

This function is defined in terms of array-axis-expand.

syntax

(for/matrix: m n maybe-fill (for:-clause ...) maybe-type-ann
  body ...+)

syntax

(for*/matrix: m n maybe-fill (for:-clause ...) maybe-type-ann
  body ...+)
 
maybe-fill = 
  | #:fill fill
     
maybe-type-ann = 
  | : body-type
 
  m : Integer
  n : Integer
  fill : body-type
Like for/array: and for*/array:, but for matrices. The only material difference is that the shape m n is required and must be positive.

syntax

(for/matrix m n maybe-fill (for-clause ...)
  body ...+)

syntax

(for*/matrix m n maybe-fill (for-clause ...)
  body ...+)
Untyped versions of the loop macros.

  top  ← prev  up  next →